Orthogonalized B-splines — orthogonize_bspline • QuantRegGLasso

Generate a set of orthogonalized B-splines using the Gram-Schmidt algorithm applied to the built-in function splines::bs().

orthogonize_bspline(
  knots,
  boundary_knots,
  degree,
  predictors = NULL,
  is_approx = FALSE
)

Arguments

knots: Array. The knots that define the spline.
boundary_knots: Array. The breakpoints that define the spline.
degree: Integer. The degree of the piecewise polynomial.
predictors: Array. The predictor variables with size p.
is_approx: Boolean. The default is FALSE.

Value

A list containing:

bsplines: Matrix of orthogonalized B-splines with dimensions \((p, \text{length}(knots) + \text{degree} + 1)\)
z: Predictors used in generation

Examples

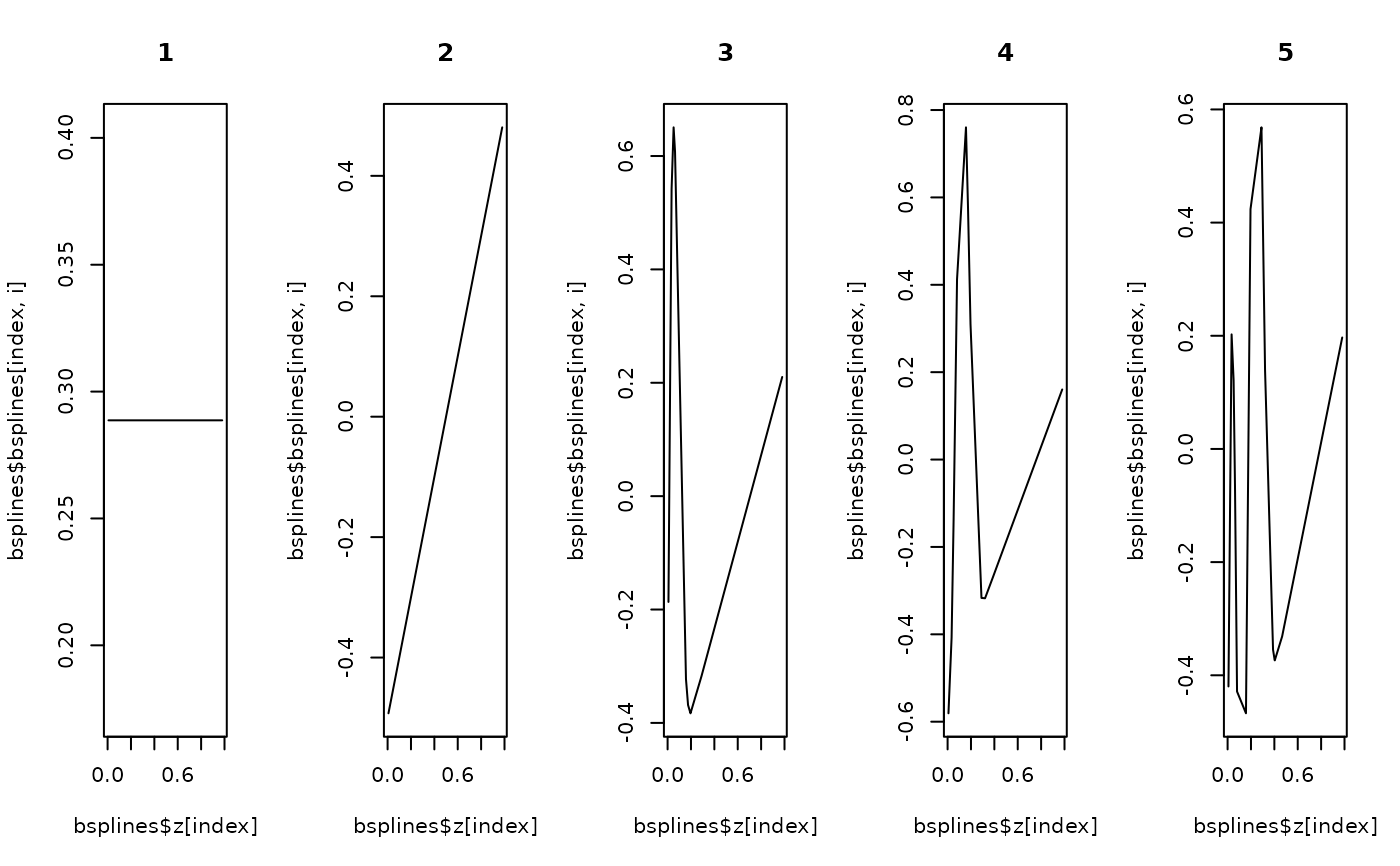
# Example: Generate and plot the first 5 orthogonalized B-splines
p <- 30
total_knots <- 10
degree <- 3
boundaries <- c(0, 1)
x <- seq(from = 0, to = 1, length.out = total_knots)
knots <- x[2:(total_knots - 1)]
predictors <- runif(p, min = 0, max = 1)
bsplines <- orthogonize_bspline(knots, boundaries, degree, predictors)

# Plot the first 5 B-splines
index <- order(bsplines$z)
original_par <- par(no.readonly = TRUE)
par(mfrow = c(1, 5))
for (i in 1:5)
  plot(bsplines$z[index], bsplines$bsplines[index, i], main = i, type = "l")

par(original_par)