個人資料去識別化
在這提倡開放資料(open data)的時代,各機構從資料收集、維護到能夠公開分享,如何妥善的保護資料中的個人隱私是個廣泛討論的議題。例如,使用者希望政府資料能夠增加資料的透明程度以及增加新的資訊而增加資料的可用性,進而可以提供政府更有效的決策。為了確保隱私,避免暴露其身份,從圖1我們可以清楚了解資料收集個人資訊到最終分享資料的流程。當中,在公開資料前為了達到隱私保護的效果,必須對於資料執行適當保護措施 – 去識別化(de-identification)。去識別化是讓機構能夠從自己資料庫移除個人資訊的工具,使得其資料能二次使用或是分享給其他機構做學術或是商業相關的研究用途。
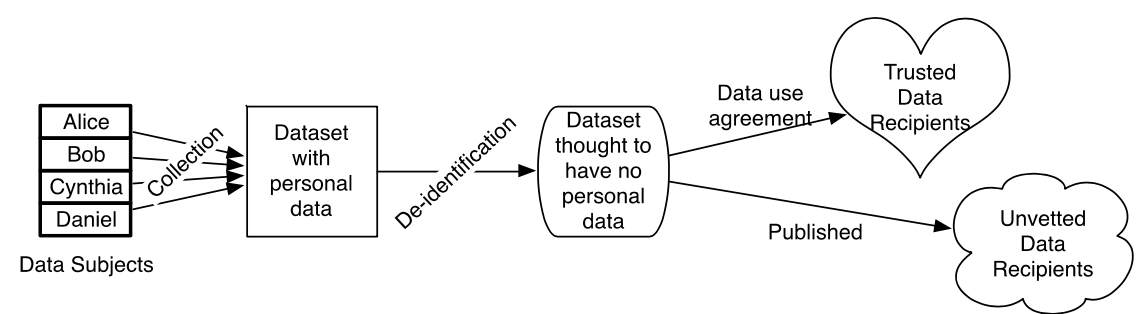
去識別化並非只依靠單一的技術,而是針對不同需求或是法令之下,同時使用一些數值方法及演算法保護資料的個人隱私。例如,美國對於醫療紀錄上訂定在健康保險中的Accountability Act (HIPAA) Privacy Rule; 台灣公布的個資法案第二條中指出,企業或是機構需防止直接或間接方式識別個人資料,如自然人之姓名、國民身分證統一編號、護照號碼等。過去常用的去識別化方法包含(1)刪除或是隱藏個人身份指標,例如:姓名和身份證號碼; (2) 泛化(generalization)或是抑制(supression) 準識別符(quasi-identifiers) 例如生日或郵遞區號,其中泛化是將數值型屬性以其區間值取代,抑制通常是以符號‘*’隱藏屬性的資訊。 但攻擊者有很高可能性透過剩餘資料輔助來重新辨識資料,例如, Sweeney[10] 提到在1990年普查資料中,美國約有87%的人口能藉由郵遞區號、性別和出日來判別單一個人身份,間接地能地能夠竊取個人隱私 (見圖2)。
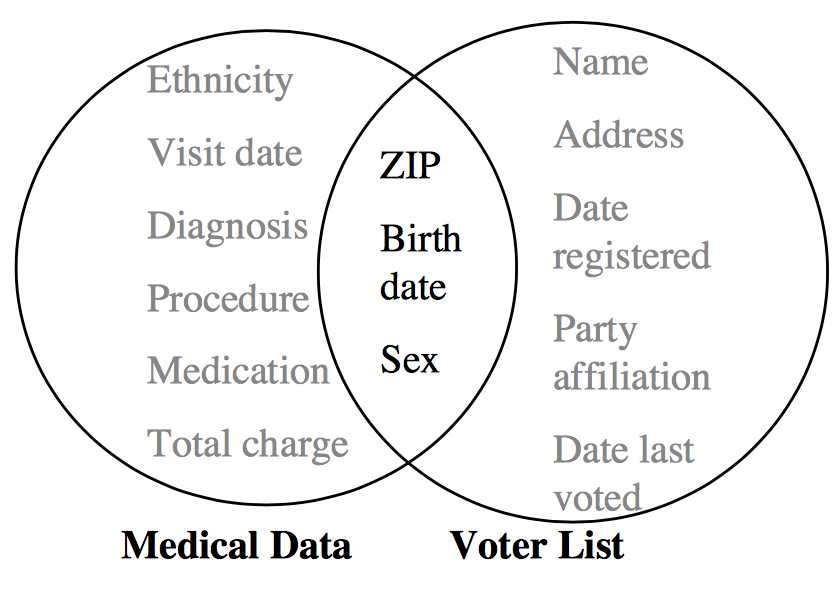
在學術上,可以將保護隱私資訊分成兩個模型(Garfinkel [5]) :
- (1) 保留隱私的資料公開(PPDP: Privacy Preserving Data Publishing);
- (2) 保留隱私的資料探勘(PPDM: Privacy Preserving Data Mining)。
在PPDP模型會將資料中個人隱私的部分直接進行處理,公開一份修改過的資料; 另一方面,資料用於PPDM模型,是將資料中身份或是敏感屬性的部分利用統計分析或是機器學習來保持資料原有的統計特性,進而將資料重新彙整公開。接下來,我們將根據這兩個模型介紹幾種不同常用的方法。
PPDP: 隨機化(Randomization)
隨機化的方法是將可以辨識的屬性中的資料,隨機的替換相對應屬性的資料而不考慮刪除或是隱藏其屬性。例如,將真實的姓名、生日、身分證號碼,從另外較大的資料庫隨機選取相對應的屬性的假資料,進而取代原本屬性中某幾筆資料。 進一步來說,隨機化可以透過一些對屬性的限制讓取代後的資料擬真度提高。例如:姓名屬性在隨機化替換過程,透過限制相同性別或是限制相同區域的姓名進行隨機抽取。 El Emam and Fineberg [3]指出此類方法的缺點為:隨機化後的資料沒辦法有效了解被重新辨識的風險,因此此資料的隱私分析需要透過自己的觀點判斷是否資料被重新辨識的可能性。
PPDP: 虛擬化假名(Pseudonymization)
虛擬化假名是利用暫時性的身份用來取代真實姓名,透過刪除或是隱藏個人身份指標來使得個人身份無法辨識,而常用的工具為雜湊函數(hash function) 。當我們使用雜湊函式在個人資訊上,我們是把訊息透夠複雜的密碼運算轉換成雜湊值(hash value)。雜湊值常用英文字母和數字隨機組成的字串表示,而且一個雜湊值只能對應一組個人資訊。例如圖3表示在臨床資料中,我們將受測者的姓名以及電話號碼以一組虛擬化假名的密碼來取代。
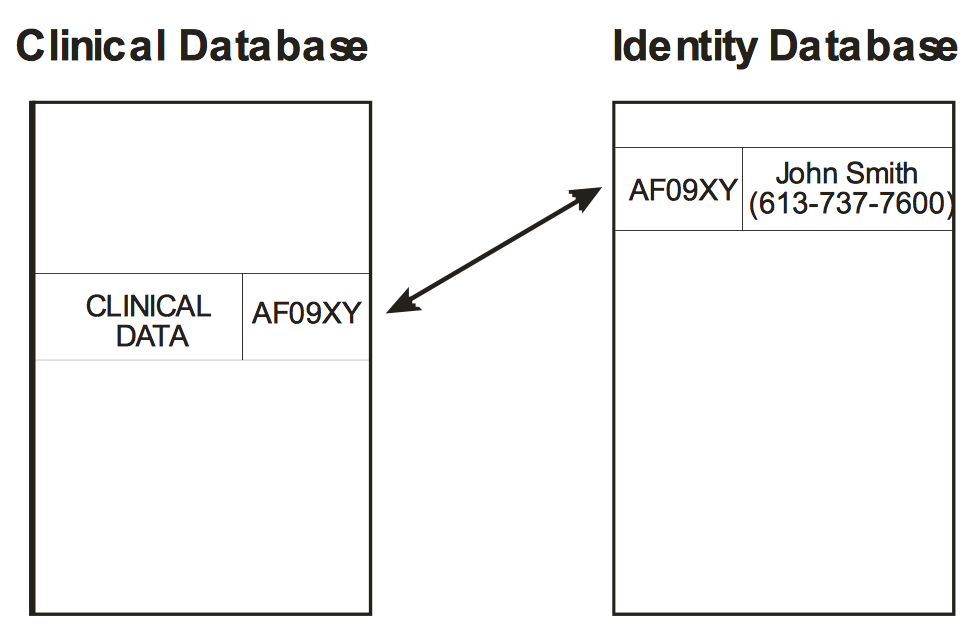
一個良好的雜湊函式通常是一個單向雜湊(one-way hash),即很難利用雜湊值去反向找到原始的訊息字串,也就是若輸入的訊息不同,它們對應到不同雜湊值的機率很高。 所以常用的雜湊函數都是可以接受位元組(bit)夠長的字串,來產生固定長度位元組密碼。依據密碼安全而言,雜湊函數能夠接受字串越長而且產生較長的雜湊值通常是較安全的。常用的雜湊函數會依據如(Eastlake 3rd and Jones [2], Khovratovich
et al. [7], Gaj et al. [4]):
MD5可以接受最大$(2^{64}-1)$ 位元組長度的訊息字串,輸出長度$128$位元組的雜湊值;
SHA-1可以接受最大$(2^{64}-1)$ 位元組長度的訊息字串,輸出長度$160$位元組的雜湊值;
SHA-256 - 可以接受最大$(2^{64}-1)$ 位元組長度的訊息字串,輸出長度$256$位元組的雜湊值;
SHA-512 - 可以接受最大$(2^{128}-1)$ 位元組長度的訊息字串,輸出長度$512$位元組的雜湊值。
例如 我們得到的使用者資訊為“陳金鋒 (ccf52@baseballhalloffame.org)”,
我們可以透過雜湊函數: MD5 和SHA-1得到相對應的雜湊值在表1在,其中我們是利用統計軟體R的套件digest來計算雜湊值。
| 姓名 | ||
|---|---|---|
| 真實資料 | 陳金鋒 | ccf52@baseballhalloffame.org |
| MD5 雜湊值 | 475a5745a3c74e6e7fd970d3ed7e584e | f7428ff3416a3b08fe958f2ab696df4 |
| SHA-1 雜湊值 | 3f222f61e1a5add6c9e64818e5cc9cb4bee2b4ee | 44a5387e6e079cbdf6305137b8dfea73b299c64c |
PPDP: $k$-匿名($k$-anonymity)
Sweeney [10] 提出 $k$-匿名($k$-anonymity) 演算法用於防止鏈結攻擊(linking attack)透過在其他資料中有相似的紀錄而竊取個人隱私。其方法是透過修改資料表中準識別符屬性(泛化或是抑制),使得資料表中至少$k-1$筆資料無法與所選的的資料在區隔,即與所選的資料相同。因此無法直接或是間接重新識別身份。例如,表2是原始資料表、表3是將準識別符資訊隱藏的3-匿名化資料表,其中郵遞區號是經過抑制轉換,年齡是經過抑制以及泛化轉換。
| 郵遞區號 | 年齡 | 違規項目 | |
|---|---|---|---|
| 1 | 23123 | 30 | 酒駕 |
| 2 | 23131 | 32 | 酒駕 |
| 3 | 23111 | 37 | 酒駕 |
| 4 | 11021 | 45 | 超速 |
| 5 | 11023 | 50 | 超速 |
| 6 | 11022 | 63 | 超速 |
| 7 | 12321 | 22 | 酒駕 |
| 8 | 12311 | 23 | 未戴安全帽 |
| 9 | 12301 | 19 | 紅燈右轉 |
| 郵遞區號 | 年齡 | 違規項目 | |
|---|---|---|---|
| 1 | 231** | 3* | 酒駕 |
| 2 | 231** | 3* | 酒駕 |
| 3 | 231** | 3* | 酒駕 |
| 4 | 110** | $\geq 45$ | 超速 |
| 5 | 110** | $\geq 45$ | 超速 |
| 6 | 110** | $\geq 45$ | 超速 |
| 7 | 123** | $< 30$ | 酒駕 |
| 8 | 123** | $< 30$ | 未戴安全帽 |
| 9 | 123** | $< 30$ | 紅燈右轉 |
當$k$值越大,資料隱私被保護效果越好,但相對的,資料失真的程度亦高,進而造成資料的研究可用性降低。因此如何選取適當的K值,是非常複雜的問題。
然而,$k$-匿名方法仍有許多不完備之處。Machanavajjhala et al. [9]指出對於敏感資料中,兩種$k$-匿名可能遭受的攻擊。首先是同質性攻擊(homogeneity attach),攻擊者可以透過資料敏感屬性中的些微差異來復原原來的敏感屬性。例如,表3 中的敏感屬性為違規項目 ,若攻擊者知道某人年齡32歲住在郵遞區號23131,可以間接推斷他有酒駕。其二是背景知識攻擊(background knowledge attack),攻擊者對原先資料的背景知識有一定程度了解,進而透過敏感資訊與個人關係來還原資料。。例如,攻擊者知道李四的年齡及居住地在表3的最後一個區塊,且知道李四不喝酒只開車,可以間接推斷李四可能紅燈右轉。為了防止這些攻擊,Machanavajjhala et al. [9]提出$\ell$多樣性($\ell$-diversity)改善了$k$-匿名,保證任意一個等價類中的敏感屬性都至少有$\ell$個不同的值。更進一步的,Li et al. [8] 根據$\ell$-diversity 提出$t$-Closeness,要求所有等價類中敏感屬性的機率分布儘量接近該屬性的機率分布。
PPDM: 統計洩漏控制流程(Statistical Disclosure Control Process)
統計洩漏控制流程是預防資料庫中公開提供統計分析的微資料(microdata)被用來識別資料的身份及隱私 ,常用的方法為多維度微聚合(multivariate microaggregation)。多維度微聚合與$k$-匿名方法不同之處在於微聚合修改資料不需要透過泛化或是抑制,而是將微資料進行分群(clustering),每一群體都至少有 $k$ 筆資料,以每一群體的中心位置(如平均數或是中位數)來取代該群內的記錄。 此類的微聚合是透過最大距離到平均向量(Maximum Distance to Average Vector)演算法實現[1]。其他多維度微聚合分群的演算法是透過不同的距離尺度來分類,如根據 馬氏距離(Mahalanobis distance)的演算法、或是根據相關係數矩陣的主成份分析(Princiapl Component Analysis) (Hundepool et al. [6])。
References
-
[1] Josep Domingo-Ferrer and Josep Maria Mateo-Sanz. Practical data-oriented microaggregation for statistical disclosure control. IEEE Transactions on Knowledge and data Engineering, 14(1):189–201, 2002.
-
[2] D Eastlake 3rd and Paul Jones. Us secure hash algorithm 1 (sha1). Technical report, 2001.
-
[3] Khaled El Emam and Anita Fineberg. An overview of techniques for de-identifying personal health information. Access to Information and Privacy Division of Health Canada, 2009.
-
[4] Kris Gaj, Ekawat Homsirikamol, and Marcin Rogawski. Comprehensive comparison of hardware performance of fourteen round 2 sha-3 candidates with 512-bit outputs using field programmable gate arrays. In 2nd SHA-3 Candidate Conference, Santa Barbara, August, pages 23–24, 2010.
-
[5] Simson L Garfinkel. De-identification of personal information. National Institute of Standards and Technology, Gaithersburg, MD, Tech. Rep. IR-8053, 2015.
-
[6] Anco Hundepool, Josep Domingo-Ferrer, Luisa Franconi, Sarah Giessing, Eric Schulte Nordholt, Keith Spicer, and Peter-Paul De Wolf. Statistical disclosure control. John Wiley & Sons, 2012.
-
[7] Dmitry Khovratovich, Christian Rechberger, and Alexandra Savelieva. Bicliques for preimages: attacks on skein-512 and the sha-2 family. In Fast Software Encryption, pages 244–263. Springer, 2012.
-
[8] Ninghui Li, Tiancheng Li, and Suresh Venkatasubramanian. t-closeness: Privacy beyond $k$-anonymity and $\ell$-diversity. In Data Engineering, 2007. ICDE 2007. IEEE 23rd International Conference on, pages 106–115. IEEE, 2007.
-
[9] Ashwin Machanavajjhala, Daniel Kifer, Johannes Gehrke, and Muthuramakrishnan Venkitasubramaniam. $\ell$-diversity: Privacy beyond $k$-anonymity. ACM Transactions on Knowledge Discovery from Data (TKDD), 1:3, 2007.
-
[10] Latanya Sweeney. k-anonymity: A model for protecting privacy. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 10(05):557–570, 2002.