Capture the Dominant Spatial Pattern with One-Dimensional Locations
Wen-Ting Wang
Source:vignettes/demo-one-dim-location.Rmd
demo-one-dim-location.RmdObjective
We have two objectives 1. Demonstrate how SpatPCA captures the most dominant spatial pattern of variation based on different signal-to-noise ratios. 2. Represent how to use SpatPCA for one-dimensional data
Basic settings
Used packages
library(SpatPCA)
library(ggplot2)
base_theme <- theme_classic(base_size = 18, base_family = "Times")True spatial pattern (eigenfunction)
The underlying spatial pattern below indicates realizations will vary dramatically at the center and be almost unchanged at the both ends of the curve.
set.seed(1024)
position <- matrix(seq(-5, 5, length = 100))
true_eigen_fn <- exp(-position^2) / norm(exp(-position^2), "F")
plot_df <- data.frame(position = position, eigenfunction = true_eigen_fn)
ggplot(plot_df, aes(position, eigenfunction)) +
geom_line() +
base_theme
Case I: Higher signal of the true eigenfunction
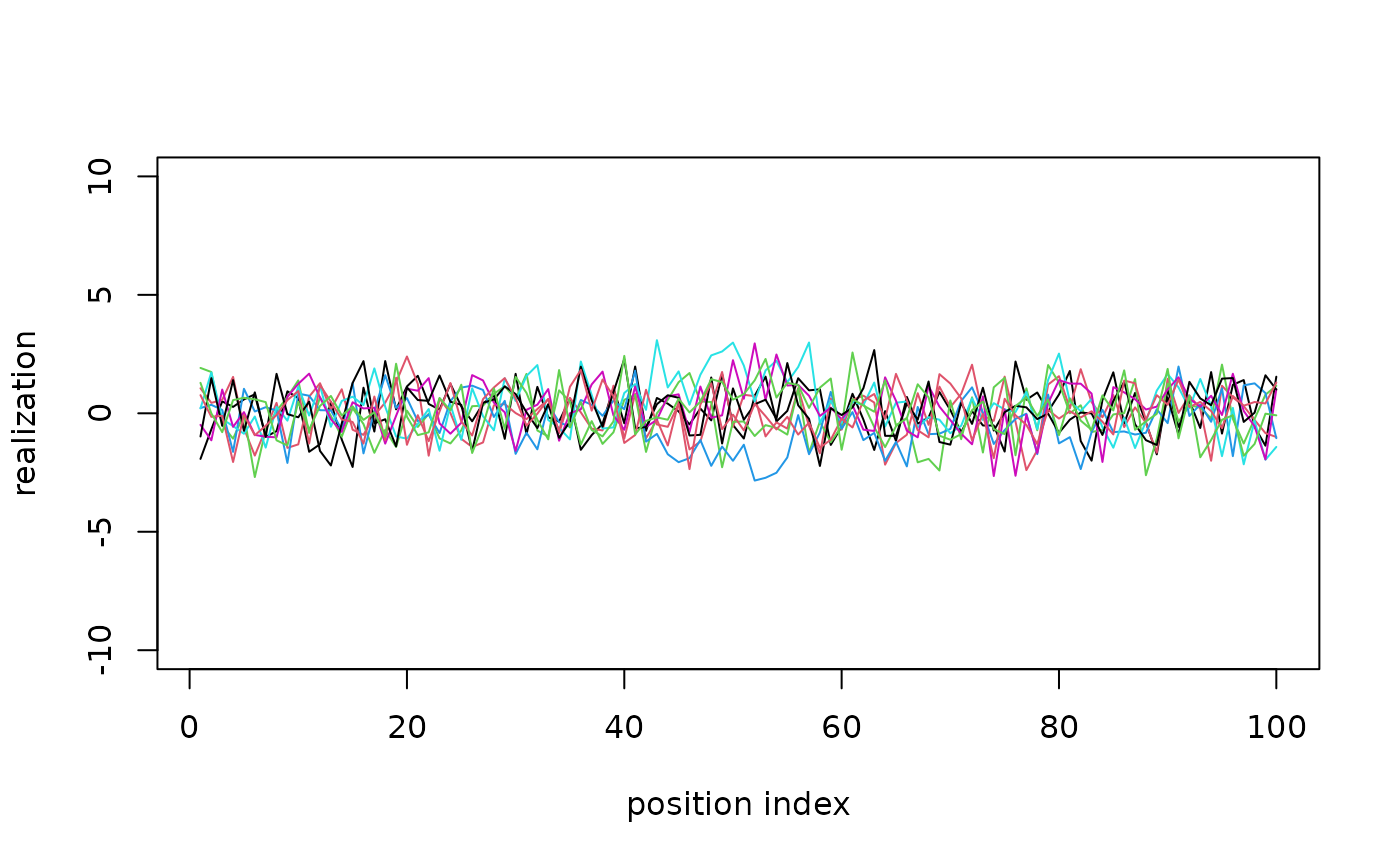
Generate realizations
We want to generate 100 random sample based on - The spatial signal for the true spatial pattern is distributed normally with - The noise follows the standard normal distribution.
Animate realizations
We can see simulated central realizations change in a wide range more frequently than the others.
subset_idx <- seq(1, 100, length.out = 9)
matplot(
t(realizations[subset_idx, ]), type = "l", lty = 1,
ylim = c(-10, 10),
xlab = "position index", ylab = "realization"
)
Apply SpatPCA::spatpca
cv <- spatpca(x = position, Y = realizations)
eigen_est <- cv$eigenfnCompare SpatPCA with PCA
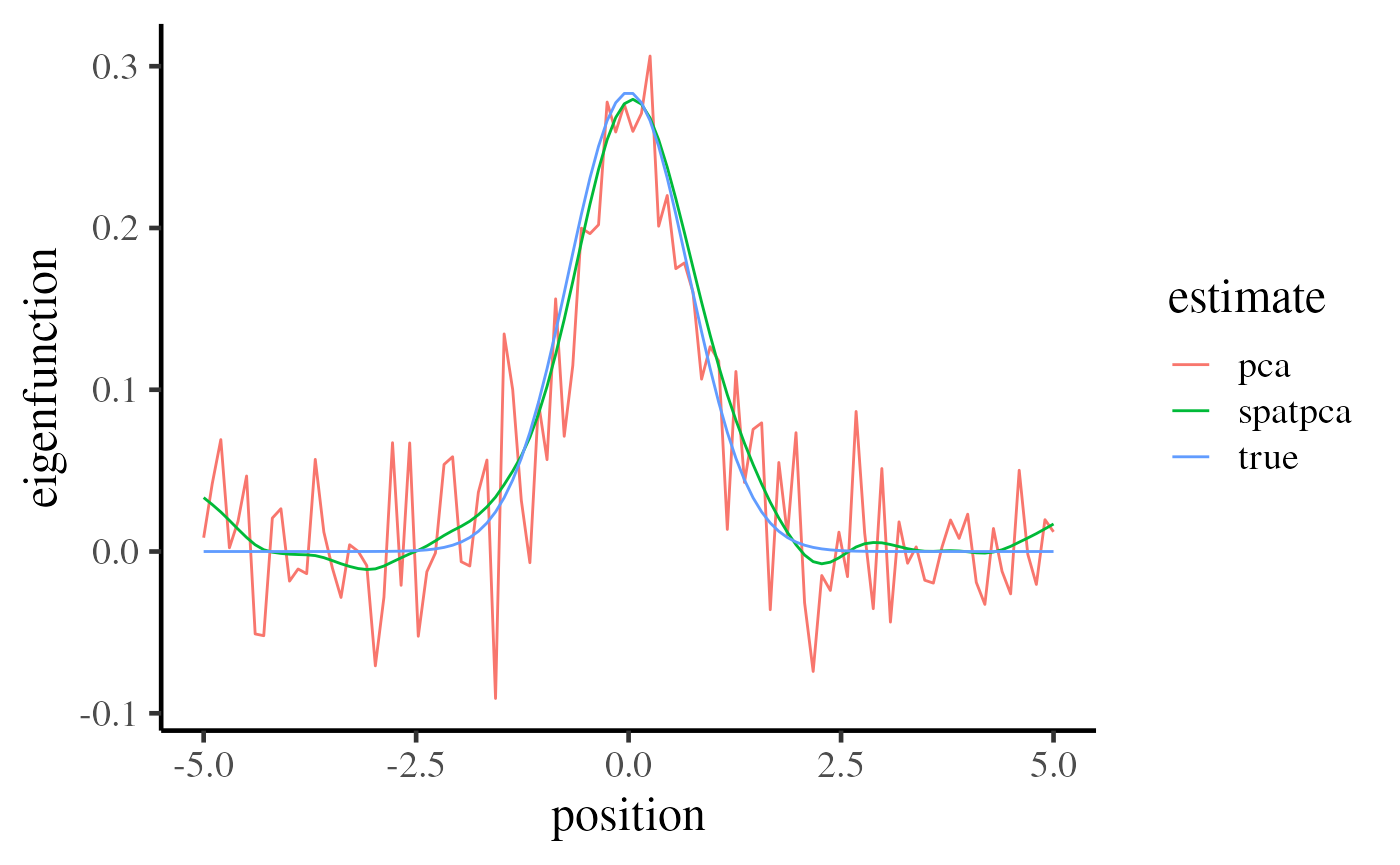
There are two comparison remarks 1. Two estimates are similar to the true eigenfunctions 2. SpatPCA can perform better at the both ends.
plot_df <- data.frame(
position = position,
true = true_eigen_fn,
spatpca = eigen_est[, 1],
pca = svd(realizations)$v[, 1]
)
plot_df_long <- data.frame(
position = rep(plot_df$position, 3),
estimate = rep(c("true", "spatpca", "pca"), each = nrow(plot_df)),
eigenfunction = c(plot_df$true, plot_df$spatpca, plot_df$pca)
)
ggplot(plot_df_long, aes(x = position, y = eigenfunction, color = estimate)) +
geom_line() +
base_theme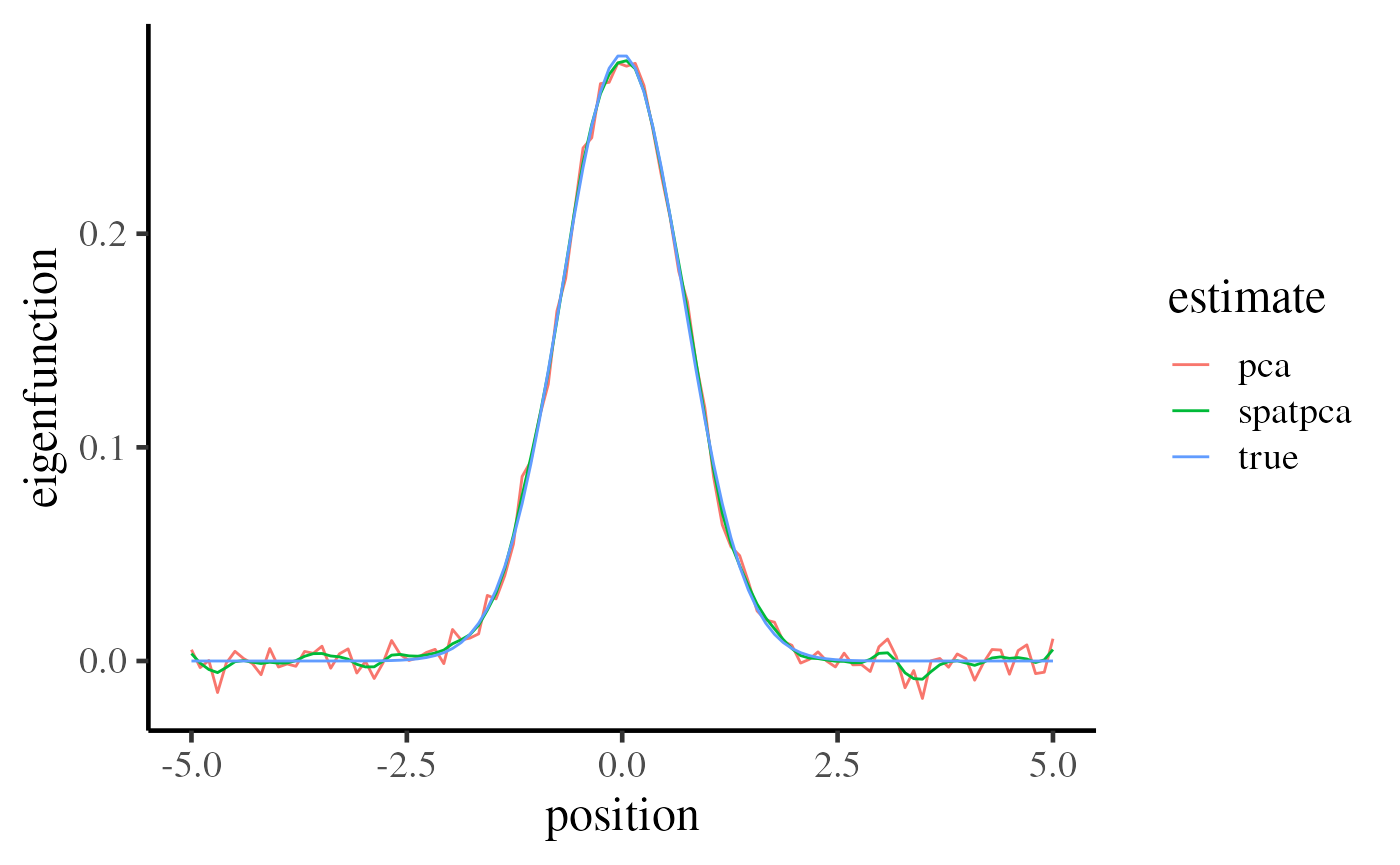
Case II: Lower signal of the true eigenfunction
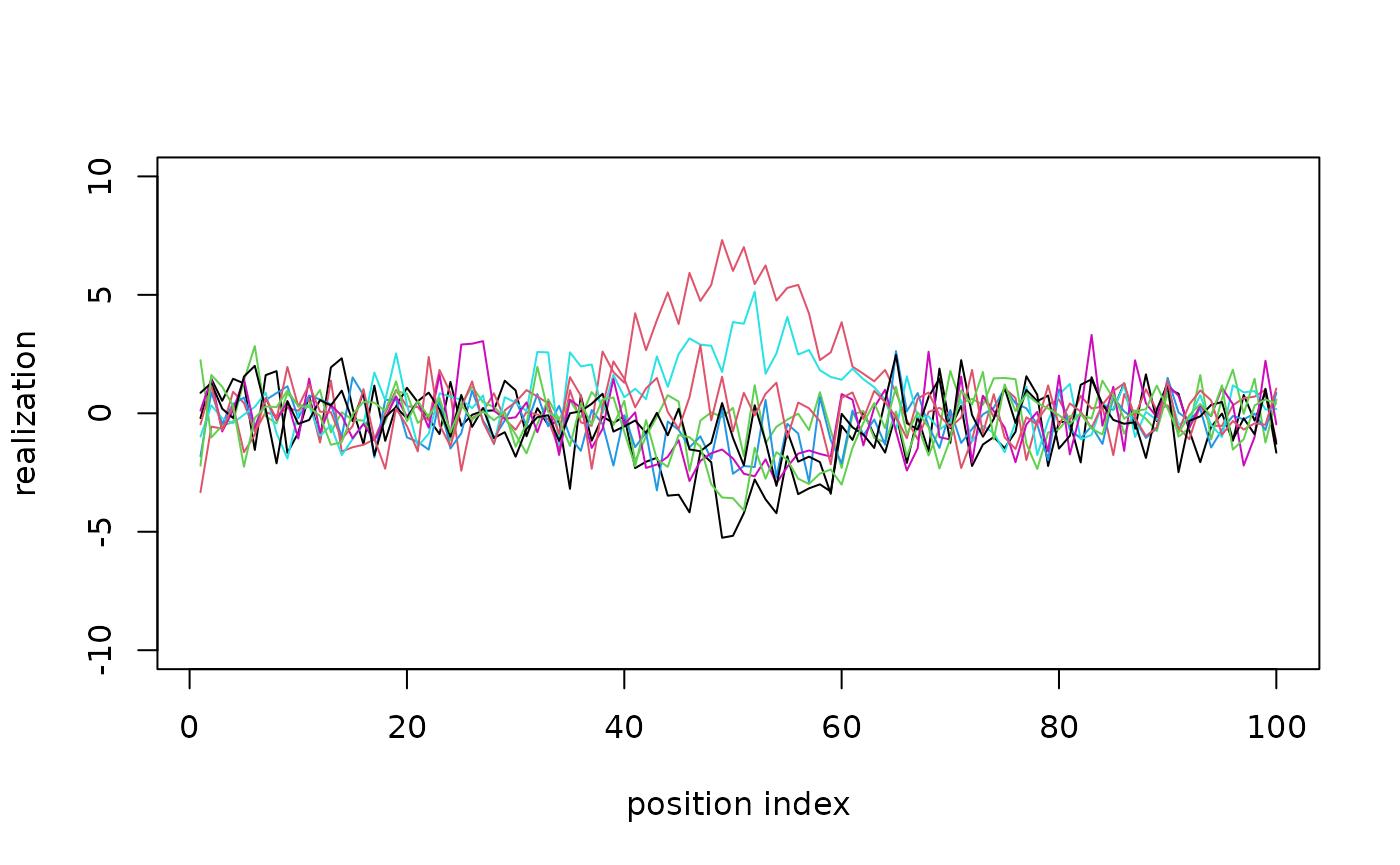
Animate realizations
It is hard to see a crystal clear spatial pattern via the simulated sample shown below.
subset_idx <- seq(1, 100, length.out = 9)
matplot(
t(realizations[subset_idx, ]), type = "l", lty = 1,
ylim = c(-10, 10),
xlab = "position index", ylab = "realization"
)
Compare resultant patterns
The following panel indicates that SpatPCA outperforms to PCA visually when the signal-to-noise ratio is quite lower.
cv <- spatpca(x = position, Y = realizations)
eigen_est <- cv$eigenfn
plot_df <- data.frame(
position = position,
true = true_eigen_fn,
spatpca = eigen_est[, 1],
pca = svd(realizations)$v[, 1]
)
plot_df_long <- data.frame(
position = rep(plot_df$position, 3),
estimate = rep(c("true", "spatpca", "pca"), each = nrow(plot_df)),
eigenfunction = c(plot_df$true, plot_df$spatpca, plot_df$pca)
)
ggplot(plot_df_long, aes(x = position, y = eigenfunction, color = estimate)) +
geom_line() +
base_theme